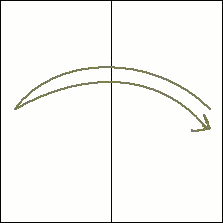To start, take a square piece of paper and fold it in half vertically. Then open it back up leaving a crease in the middle.

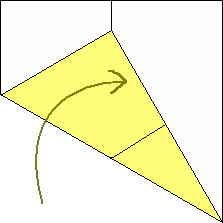Now the tricky part, where accuracy is both very difficult and very important. Bring the bottom left corner up to meet that crease you just created in such a way that the bottom edge of the paper forms a line that goes from the bottom right corner to that middle crease (Left and right are interchangable here). Difficult to explain verbally, but the diagram should hopefully clarify that.

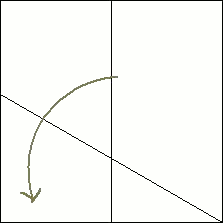Then, open that fold back up. That should leave you with two creases, one that runs vertically down the middle of the paper, and one that forms a 30° angle between itself and the bottom edge of the paper.

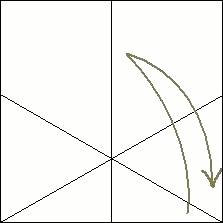Using the same method explained in steps two and three, make a crease that is a reflection of the previous one. You'll notice that this leaves the paper nicely divided into 60° angles.

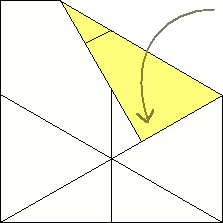Now fold the top right corner down so that the right edge lines up with the crease that comes from the bottom left corner.

Unfold it, leaving the creases displayed here.

Repeat the previous two steps on the other side of the paper.

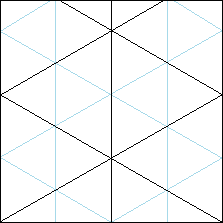You now have the basic pattern with your paper divided into equilateral triangles. From here on, you can get more triangles by subdividing the areas on the paper with reference to the creases you've already made.

It is important to note that the diagonal creases at the top of the paper will not actually meet at that point. It is impossible for that to happen on a square piece of paper. In order for them to line up perfectly, the paper would have to be a different rectangle (such as 1 X 1.0136).